PhD: Individually tailored digital-motor outcomes in real life
My Background
My background in Tübingen

| Until 2018 |
B.Sc. in Computer Science |
| Until 2021 |
M.Sc. in Computer Science |
| Until 2024 |
Research Assistant in Cognitive Science |

CCVEP decoding

Tools I like to work with
My background in Bologna

| Since June 2024 |
PhD in Health & Technologies |

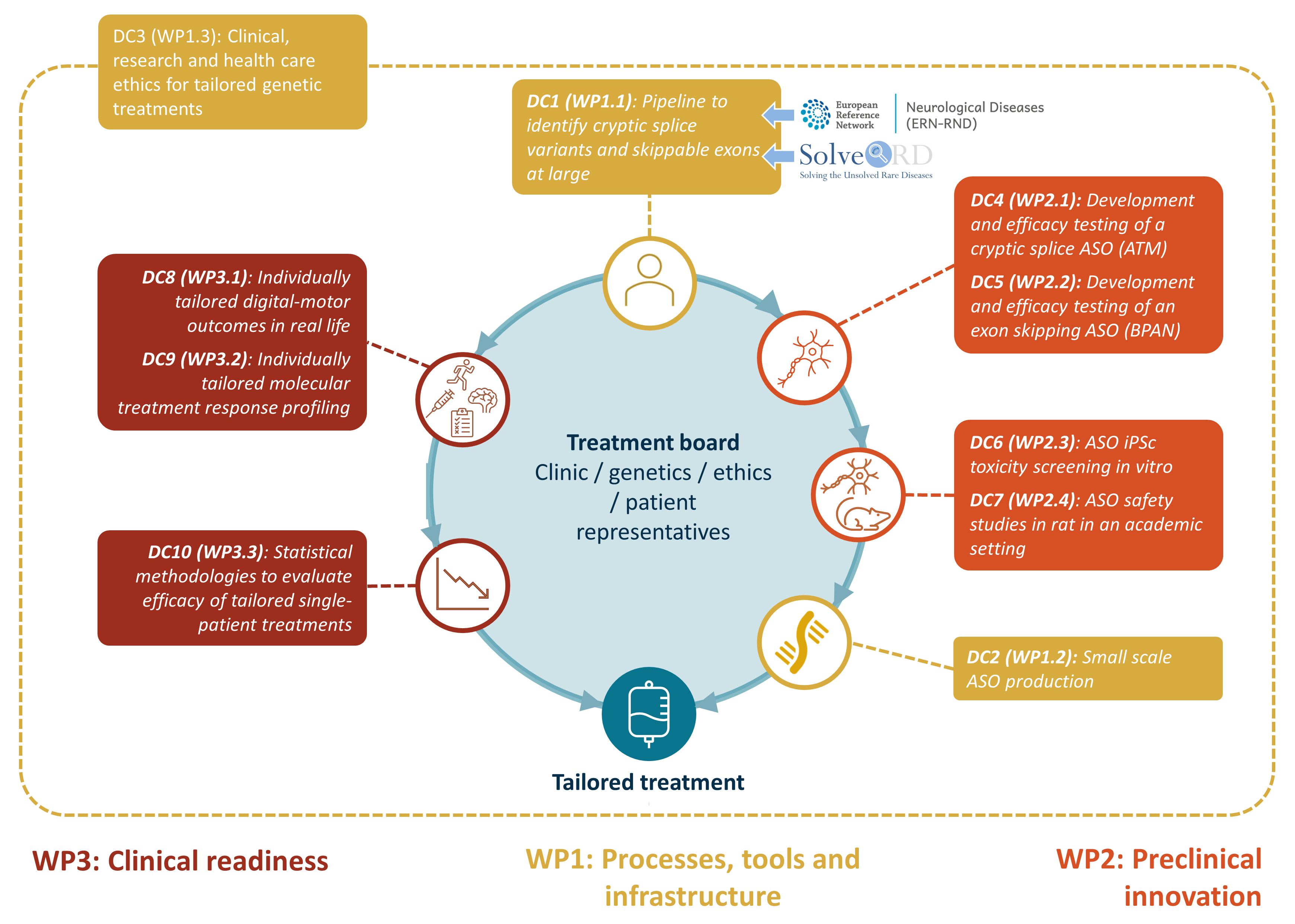
Medicine Made to Measure (MMM)
- Doctoral network
- Funded by the Marie Curie Actions Scheme
- 10 PhD candidates
- 22 participating organisations
- Aim: to develop
- Antisense oligonucleotide treatments (ASOs)
- Tailored to single patients with nano-rare disease mutations

MMM group photos

First General Assembly – Barcelona, June 2024

Mid-Term Meeting – Tübingen, December 2024
Rare diseases
- A rare disease is any disease with a
prevalence of <0.05%.
- There are >6000 rare diseases.
- Taken together, their prevalence is ~4%.
- >70% have genetic causes.
- Nano-rare mutations: Worldwide
<30 patients.
(approximate numbers, for Europe)
“rare individually, common collectively”
MMM pipeline
Supervisors

Dr. Sabato Mellone
University of Bologna

Prof. Dr. Matthis Synofzik
University of Tübingen

Prof. Dr. Mats Karlsson
University of Uppsala
Co-supervisors

Carlo Tacconi
mHealth Technologies s.r.l., Bologna

Prof. Dr. Lorenzo Chiari
University of Bologna
Secondments
- Tübingen, Germany
- Sep 2024 - Nov 2024
- Three more months in the coming years
Introduction
Individualized ASOs for nano-rare mutations:
Trial design challenges
- ASO treatment is taylor-made for the mutation
- Tiny number of patients worldwide
- ASO treatment has slow, disease-modifying effect
- Traditional clinical trial designs infeasible
- Traditional N-of-1 trial designs infeasible
Spinocerebellar Ataxia (SCA)
- Inherited neurodegenerative disease
- Affects the cerebellum and spinal cord
- Rare disease: ≤5 people per 100,000
- Increased gait variability
PhD Objective
- Robust assessment of motor performance in genetic ataxias
- Based on body-worn sensor recordings in real-life settings
- Sensitive to moderate-term change in a single patient
Deliverables
| D3.1 |
Outcomes of the large cohort study
Completed Jan 2025
|
| D3.2 |
Outcomes of focused study
Due May 2027 (postponed)
|
| D3.3 |
Robust capture of n-of-1 movement changes
Due Sep 2027
|
Gait feature extraction
Inertial measurement units
- Can be attached to various body parts
- Measure movement
- Accelerometer
- Gyroscope
- (Magnetometer, Barometer, …)

Sensor configurations

Lower back and feet

Lower back only
Gait cycle analysis

Gait measures
Gait cycle analysis

Double support


Spatial and temporal analysis

Elevation at mid-swing

Foot contact angles

Circumduction

Lateral step variability

Gait cycle analysis

Spatial and temporal analysis

Elevation at mid-swing

Foot contact angles

Circumduction

Lateral step variability

Walking bouts
- Continuous sequences of steps
- Delimited by periods of non-walking

Precise definitions vary. Typical criteria:
- Minimum length (number of steps, duration)
- Maximum allowed pause
- Rules for turns
- Sanity checks (e.g. consistent left/right alternation)
Walking segments
Split long walking bouts evenly into segments ≥25 strides.
- Better temporal resolution and homogeneity

Additional features
Signal
Position
- Left foot
- Right foot
- Trunk
×
×
Quantity
- Acceleration
- Angular velocity
- (Magnetometer)
- (Barometer)
×
↓
↓
Feature classes
- Stride-to-stride comparisons
- Discrete transform coefficients
- …
↓
Window
- Walking bout
- Walking segment
↓
Stride-to-stride comparisons

Discrete transform coefficients

Complexity measures

Feature aggregation
Aggregate:
- Lateral feature pairs (left foot and right foot)
- Stride-wise features in each walking segment
- Segment-wise features in each session/condition
Possible aggregators:
- Arithmetic mean
- Standard deviation
- Coefficient of variation
- Median, quantiles, extrema
- Interquantile ranges
- Quartile coefficient of dispersion
- …
- Result: Many candidate outcomes, each with one value per
subject and session/condition
Feature transformation
Transform features on the per-stride, per-segment, or
per-session/condition level.
Possible transformations:
- Absolute value
- Normalization (e.g. by body height)
- nth-order differences
- Logarithm
- …
Why transform? Examples:
- We are interested in an absolute deviation, not its direction
- We are interested in stride length relative to body height
- We are interested in the difference between two strides
- We want to compare multiplicative factors
- …
Environmental context effects
- Real-life context factors are known to affect gait features
- Indoors vs. outdoors
- Type or absence of shoes
- Slope, stairs
- Ground texture
- Weather
- …
- Exogenous variables, introducing variance
- Estimateable to some degree from signal-derived proxies
Context stratification
Approach:
- Stratifiy walking segments by context proxies
- Obtain one candidate outcome per stratum
- Stratum intersections or unions possible too
| Keywords |
Covariate |
Threshold(s) |
| slow /
fast |
Gait speed |
1.2m/s |
| sporadic /
continuous |
Number of steps in a 1-minute window |
45 |
| straight /
curvy |
Number of turns in a 1-minute window |
1 |
| short /
long |
Walking bout duration |
30s |
Disadvantages:
- High feature count gets increased even more
- The more specific a stratum, the less data is considered
Context compensation
Approach:
- Fit a linear model for each per-segment feature
- Dependent variable: Feature
- Regressors: Context proxies
- Explain context-induced variance
- Without touching disease-status-induced variance
Gait feature extraction summary figure

Data
Dataset
- Gait recordings from Tübingen University Hospital
- 27 genetic spinocerebellar (pre-)ataxia patients
- 36 healthy controls
- Lab-based & real-life
- Yearly follow-ups over several years
- Patients further categorized into:
- 6 pre-symptomatic (SARA 2 ± 1)
- 21 symptomatic (SARA 10 ± 3)
- In total:
- ~200 visits
- ~20000 walking segments
- ~570,000 gait cycles
Other potential datasets
- PROSPAX
- Lab-based movement recordings only
- ≥74 ARSACS (spastic ataxi) patients
- ≥113 SPG7 (spastic paraplegia) patients
- ≥50 healthy controls
- Planned prospective study
- ≥10 ataxia (SCA or AT) patients
Outcomes
- Clinician- / patient-rated scores (per visit)
- SARA
- ABC
- Others, but incomplete (SPRS, INAS, PGI, ADL)
- Digital motor outcomes
- Large space of combinations, small fraction suitable
Further covariates
- Demographics (age, gender)
- Diagnosis / gene affected
- Anthropometrics at first visit (weight, height, handedness, …)
- Estimated age of disease onset (only 19 of 27 patients)
SARA score
“Scale for the assessment and rating of ataxia”
| Item |
Possible responses |
| 1) Gait |
0 - 8 |
| 2) Stance |
0 - 6 |
| 3) Sitting |
0 - 4 |
| 4) Speech disturbance |
0 - 6 |
| 5) Finger chase |
0 - 4 |
| 6) Nose-finger test |
0 - 4 |
| 7) Fast alternating hand movements |
0 - 4 |
| 8) Heel-shin slide |
0 - 4 |
| Total |
0 - 40 |
ABC score
“Activities-specific balance confidence scale”
How confident are you that you will not lose your balance or become
unsteady when you…
- …walk around the house?
- …walk up or down stairs?
- …bend over and pick up a slipper from the floor?
- …
- Traditionally 16 items
- In the Tübingen dataset: extended to 41 items
Disease onset estimates

Tezenas du Montcel et al. 2014
Data: Per-visit level

SARA scores in healthy subjects simulated (based on Shaafi Kabiri et al.
2018)
Data: Per-visit level

Data: Per-visit level

Qualitative characteristics
- Generally constant over time in the absence of disease
- Effect of age, if present, is small
- Roughly linear rise at disease onset
- Theoretical saturation not/barely represented in the dataset
- Clinical scales bounds not reached
- DMOs said to saturate around SARA 12-15
Data are potentially “ill-behaved” in several ways:
- Selection/attrition bias
- Disease onset estimation error (and missingness)
- Depending on model, residuals might be:
- Heteroskedastic
- Non-normal
- Serially correlated
Data: Per-segment level

Evaluation under traditional trial design
Longitudinal paired-samples testing (Seemann
et al.)
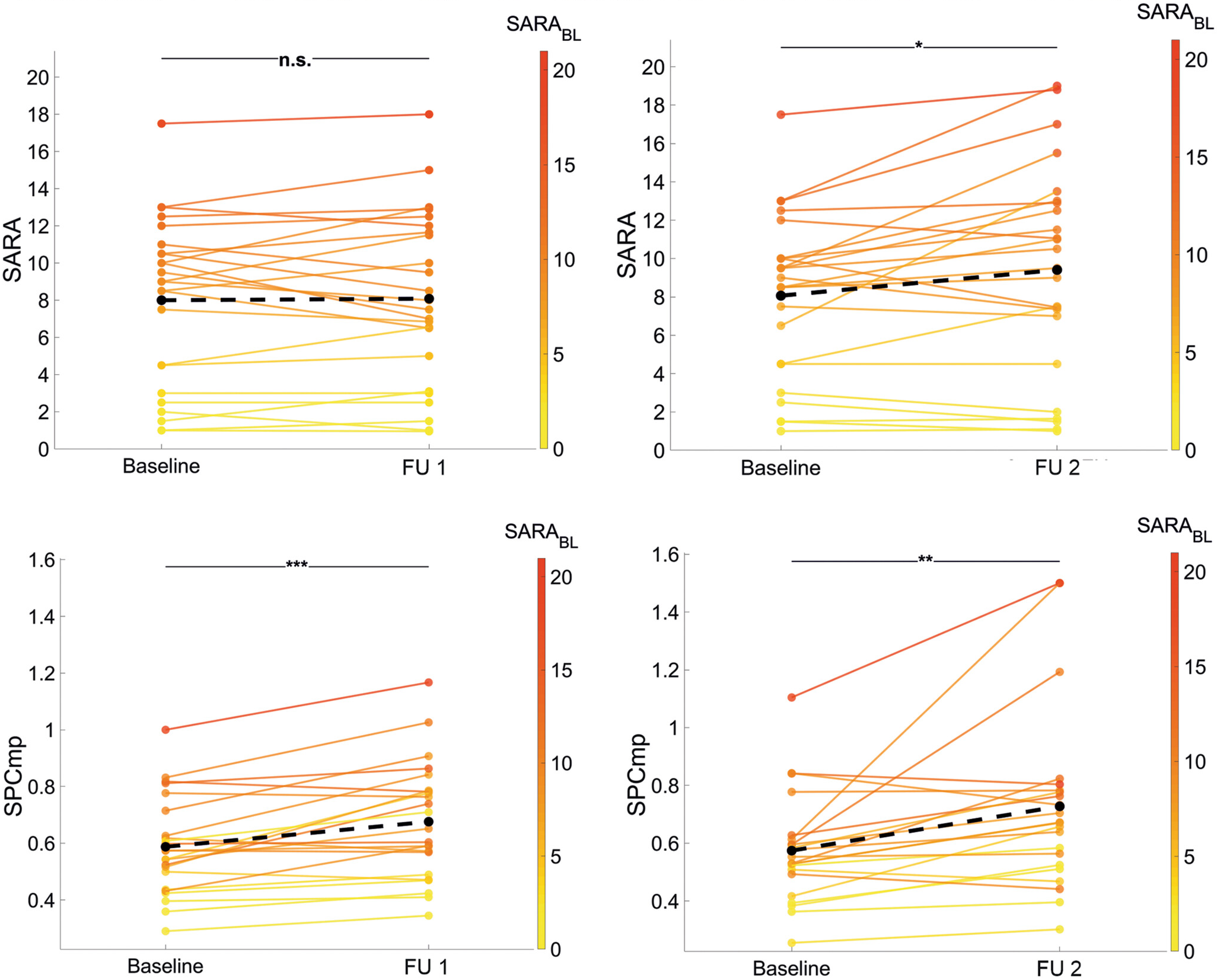
Seemann et al. 2025
Longitudinal paired-samples testing (Seemann
et al.)
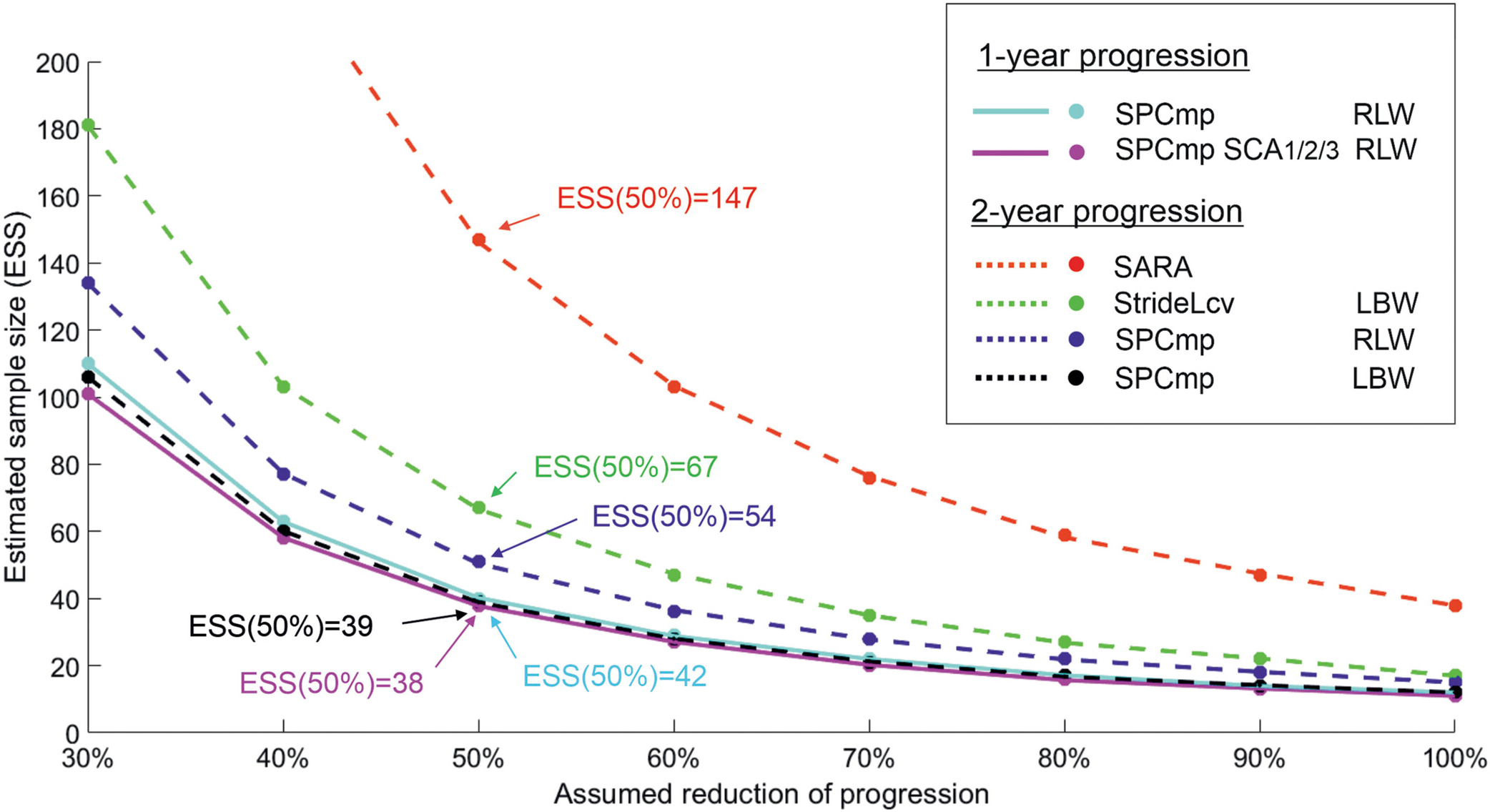
Seemann et al. 2025
Longitudinal paired-samples testing

Longitudinal paired-samples testing

Longitudinal paired-samples testing

Longitudinal paired-samples testing

Pooled sample size estimates
- Pool 1-, 2-, and 3-year effect sizes
- With inverse variance weighting
- Pre-normalize to 1-year by linear interpolation
- Assumes outcomes change linearly on average
Outcome ranking
| outcome |
ess |
rb_lgt |
rb_crs |
ρ_ΔΔ_2y |
spread |
| 1y |
2y |
3y |
sym |
sara<8 |
sara≥8 |
sara |
-abc |
| test_dw_instance_compound_5 |
39 |
.86 |
.75 |
.96 |
.68 |
.28 |
.67 |
.32 |
.12 |
|
| test_dw_instance_compound_3 |
45 |
.82 |
.66 |
.93 |
.59 |
.18 |
.62 |
.26 |
.26 |
|
| test_dw_instance_compound_2 |
55 |
.77 |
.78 |
.78 |
.49 |
.36 |
.48 |
.58 |
.21 |
|
| test_dw_instance_compound_4 |
66 |
.79 |
.65 |
.36 |
.75 |
.48 |
.52 |
.33 |
.2 |
|
| agg_adjacent_swings_resampled_sensor_lumbar_acc_x_r_d1_abs_μ /σ /curvy_long/μ |
74 |
.71 |
.45 |
.76 |
.52 |
.32 |
.46 |
-.5 |
-.06 |
.47 |
| agg_adjacent_swings_resampled_sensor_lumbar_acc_x_r_μ /σ /curvy_long/μ |
83 |
.62 |
.62 |
.67 |
.54 |
.24 |
.45 |
-.32 |
.0055 |
.45 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_μ /σ /long /μ |
86 |
.68 |
.46 |
.54 |
.5 |
.066 |
.42 |
-.036 |
.2 |
.52 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_d1_abs_μ/σ /long /μ |
88 |
.72 |
.4 |
.41 |
.49 |
.09 |
.4 |
.062 |
.32 |
.57 |
| agg_adjacent_swings_resampled_sensor_lumbar_acc_x_r_abs_μ /σ /curvy_long/μ |
88 |
.58 |
.66 |
.65 |
.54 |
.24 |
.45 |
-.3 |
.21 |
.42 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_d3_abs_μ/σ /long /μ |
89 |
.71 |
.42 |
.38 |
.48 |
.067 |
.41 |
.11 |
.093 |
.54 |
| stance_duration_μ /cv/curvy_long/μ |
90 |
.65 |
.76 |
.38 |
.63 |
.29 |
.52 |
.25 |
-.43 |
.45 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_d2_abs_μ/σ /long /μ |
93 |
.71 |
.44 |
.38 |
.48 |
.067 |
.4 |
.11 |
.21 |
.54 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_d1_abs_μ/μ /long /μ |
94 |
.62 |
.52 |
.43 |
.54 |
.12 |
.42 |
.16 |
.31 |
.44 |
| double_support_apdm_μ /σ /curvy_long/μ |
95 |
.69 |
.46 |
.49 |
.72 |
.42 |
.46 |
.13 |
-.37 |
.36 |
| coeff_swings_sensor_acc_dft_x_1_abs_μ /cv/long /μ |
95 |
.76 |
.51 |
.43 |
.71 |
.43 |
.44 |
.1 |
.044 |
.41 |
| agg_adjacent_swings_resampled_sensor_lumbar_acc_x_r_abs_d2_abs_μ/μ /curvy_long/μ |
96 |
.66 |
.5 |
.56 |
.63 |
.32 |
.49 |
-.24 |
.088 |
.42 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_d3_abs_μ/μ /long /μ |
97 |
.65 |
.49 |
.43 |
.54 |
.12 |
.42 |
.24 |
.35 |
.46 |
| swing_apdm_μ /cv/curvy_long/μ |
98 |
.72 |
.58 |
.49 |
.7 |
.36 |
.51 |
.15 |
-.32 |
.36 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_d2_abs_μ/μ /long /μ |
98 |
.64 |
.51 |
.41 |
.53 |
.11 |
.42 |
.22 |
.31 |
.43 |
| agg_adjacent_swings_resampled_sensor_lumbar_acc_z_r_abs_d3_abs_μ/γ /short /μ |
98 |
-.69 |
-.53 |
-.41 |
-.48 |
-.28 |
-.48 |
-.57 |
-.15 |
.69 |
| agg_adjacent_swings_resampled_sensor_lumbar_acc_x_r_abs_d1_abs_μ/σ /curvy_long/μ |
100 |
.66 |
.45 |
.69 |
.51 |
.31 |
.44 |
-.49 |
.071 |
.42 |
| initial_plus_mid_swing_apdm_μ /cv/curvy_long/μ |
100 |
.63 |
.69 |
.6 |
.67 |
.42 |
.42 |
-.097 |
.082 |
.38 |
| agg_adjacent_swings_resampled_sensor_lumbar_gyr_z_r_abs_μ /cv/long /μ |
100 |
.57 |
.56 |
.47 |
.5 |
.072 |
.41 |
.1 |
.15 |
.57 |
| gait_speed_apdm_μ /σ /curvy_long/μ |
100 |
.57 |
.73 |
.34 |
.44 |
.21 |
.45 |
.39 |
0 |
.42 |
| (…) |
| sara_sim_1 |
103 |
.53 |
.56 |
.76 |
1 |
.85 |
1 |
1 |
.077 |
|
| (…) |
Outcome ranking (mobgap)
Outcome ranking (gaitmap)
TODO: Incorporate gaitmap
Outcome ranking: Metrics
| ess |
1-year estimated sample size (pooled from 1-, 2-, 3-year) |
| rb_lgt |
Longitudinal effect sizes (Wilcoxon signed-rank rank biserial) |
| rb_crs |
Cross-sectional effect sizes (Mann-Whitney rank biserial) |
| ρ_ΔΔ_2y |
2-year change correlation (Spearman) |
| spread |
Measure of within-visit variation |
Outcome ranking: Filtering
Require:
- A certain ability to discriminate symptomatic patients
- A certain ability to discriminate low-SARA from higher-SARA
- Longitudinal patient p-values to be (somewhat) significant
- Reasonable number of patients considered longitudinally
- Longitudinal effects in controls to be non-significant or small
- Longitudinal and cross-sectional effects' signs to agree
Panel model of outcome trajectories
Panel model
\[
y_{ij} = \beta_1\mathrm{BOn}_{ij} + \beta_2\mathrm{BSat}_{ij} +
\beta_3\mathrm{BOn}_{ij}\left(\mathrm{EDO}_\mathrm{o}\right)_{i} +
\beta_4\mathrm{BOn}_{ij}\mathrm{Gender}_{i} +
\beta_4\mathrm{BOn}_{ij}\mathrm{BMI}_{i}
\]
- Fixed-effects panel model (= linear model with de-meaning)
- Done as a course exercise
- Non-parametric bootstrap & Monte Carlo methods employed
Fixed-effects panel model predictions

Fit results
| Outcome (lab-based) |
gait_speed_apdm_μ/μ/all/μ |
stride_length_apdm_μ/cv/all/μ |
| \(R^2\) |
0.60 |
0.50 |
| \(\mathrm{BOn}\) (\(p\)) |
-0.011 (0.92) |
0.0083 (0.32) |
| \(\mathrm{BSat}\) (\(p\)) |
-0.22 (2.2e-07) |
0.012 (0.00035) |
| \(\mathrm{BOn} \times \mathrm{Gender}\) (\(p\)) |
-0.095 (0.00028) |
0.0044 (0.041) |
| \(\mathrm{BOn} \times \mathrm{BMI}\) (\(p\)) |
-0.0061 (0.10) |
6e-04 (0.054) |
| \(\mathrm{BOn} \times \mathrm{EDO_o}\) (\(p\)) |
0.0043 (0.00013) |
-0.00053 (5.3e-08) |
| ESS |
60 |
106 |
| ESS (Seemann et al. 2025) |
66 |
67 |
Simulating outcome data
Data-generating process:
- Fix the number of patients and controls.
- Draw uniform ground-truth time since disease onset for first
visit.
- Scale time since disease onset by log-normal variation to model
ground-truth severity.
- Simulate selection bias by discarding patients above a fixed
severity threshold.
- Simulate normal disease onset estimate error in approximate
accordance with Tezenas du Montcel et al. 2014.
- Draw uniform number of visits per subject.
- Create time intervals with normal error and extrapolate
time-varying variables.
- Transform ground-truth severity by basis functions imitating
soft onset and feature saturation behavior.
- Add non-normal, serially correlated residuals with differing pre-
and post-onset variance.
Simulating outcome data

Assumption violations
Here:
- Simulated data
- No bootstrapping
Composite measures
Why composite measures?
- Many candidate outcomes, capturing variance from:
- Various aspects of disease severity
- Various nuisance factors
- Combining them into a composite score could:
- Leverage orthogonal information from different features
- Average out some of the unwanted variance
- Similar to a test battery for a clinical score
Optimized composite measures
- Idea: Formulate the search for the ideal combination of outcomes
as an optimization problem.
- E.g. Find linear combination that minimizes some loss.
- Loss: E.g. Composite change vs. disease time change.
\[
\min_\beta \sum_{i, j} \left(
\left( t_{i j} - \bar{t}_{i \cdot} \right) \cdot
I_{\mathrm{symptomatic}}(i) -
\sum_{k} \left( y_{k i j} - \bar{y}_{k i \cdot} \right) \cdot \beta_k
\right)^2 + \Omega(\beta)
\]
This is a linear regression (with optional regularizer
\(\Omega(\beta)\))
- From the de-meaned (and normalized) per-visit outcomes
- To the de-meaned time since baseline, if symptomatic
- Result \(\theta = \beta y\) is a generated regressor – likely
suboptimal compared to a jointly estimated latent variable model.
Factor analysis
- The “original” latent variable model
- Distills a set of observed variables into a few conceptual
factors
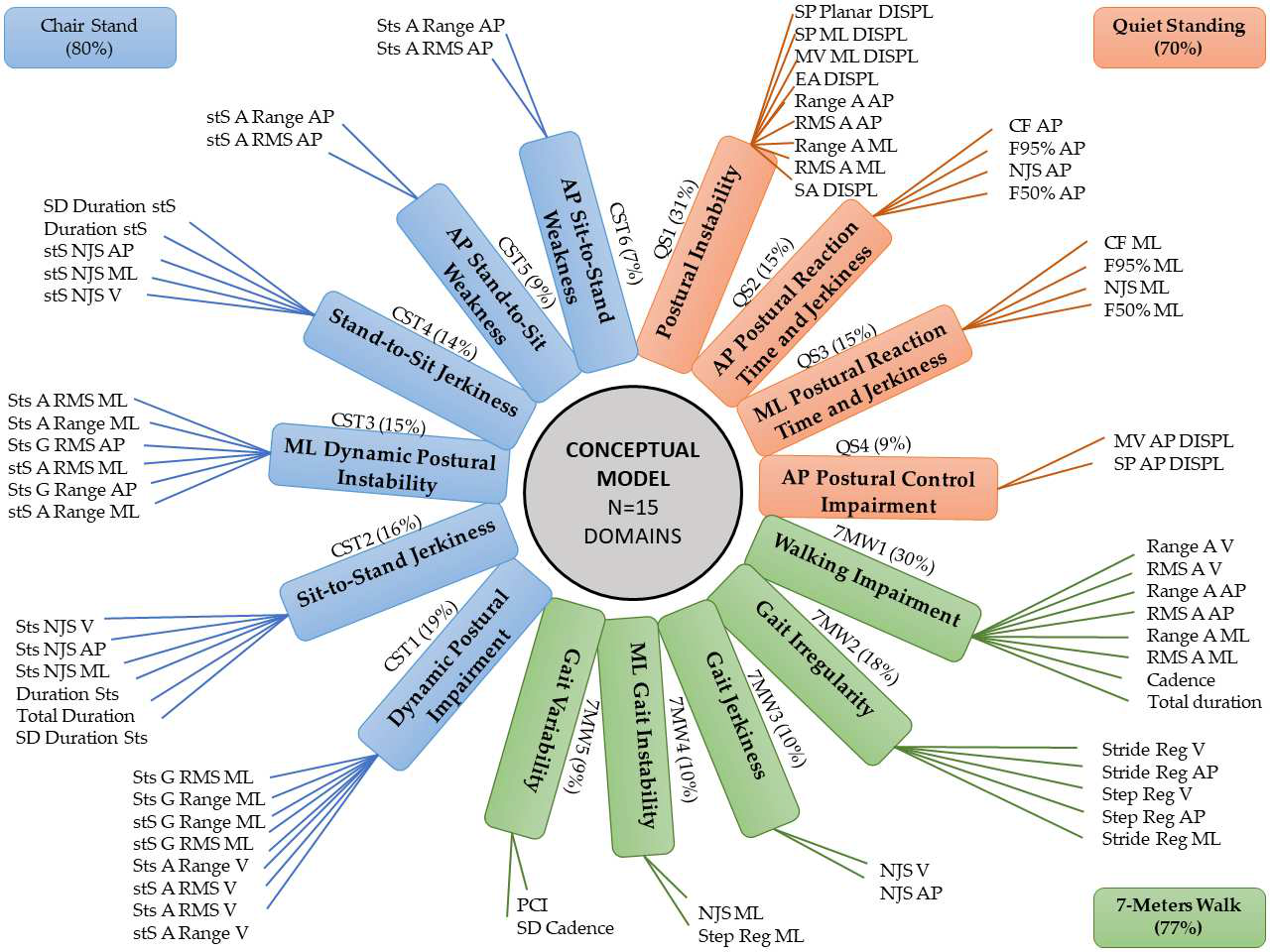
Coni et al. 2019
- Pilot test on visit level resulted in subpar composites
Cross-sectional latent disease severity modeling
Cross-sectional latent disease severity
modeling
- Model disease severity itself
- Using a non-linear, single-factor, latent variable model
- Cross-sectionally, on the segment level
- Use established relationships between features and severity for a
longitudinal model
- This has been done with success recently by Hamdan et al.
- On lab-based, visit-level features + SARA score
Item characteristic curves (Hamdan et al.)

Hamdan et al. 2024
Fisher information (Hamdan et al.)

Hamdan et al. 2024
ccIRT model performance (Hamdan et al.)

Hamdan et al. 2025
ccIRT model performance (Hamdan et al.)

Hamdan et al. 2025
Model overview
- Bayesian non-linear single-factor model
- “Cross-sectional”, i.e. considers each visit as an
individual
- Relates segment-level features to the latent disease severity
- By fitting a non-linear function per feature
- No incorporation of clinical scores
\[
y_{ij} = f\left(s_{v(i)}, \gamma_j\right) \, \beta_j + \alpha_j +
\epsilon_{ij} \qquad \epsilon_{ij} \sim t_\nu\left(0,
\sigma^2_j\right), \, s_v \sim \mathcal{N}(0, 1)
\]
Where:
- \(j\) enumerates features
- \(i\) enumerates walking segments
- \(v(i)\) is the visit to which walking segment \(i\) belongs
- \(s_{v(i)}\) is the severity at visit \(v(i)\)
Choice of \(f\)
\[ \begin{align}
\mathrm{exprel}(x) &= \frac{e^x - 1}{x} \\
\mathrm{tilt}(x, \gamma) &= x \, \mathrm{exprel}(\gamma x) \\
f(x, \gamma) &= \mathrm{tilt}(x, \gamma) \, \mathrm{scale}(\gamma) +
\mathrm{offset}(\gamma)
\end{align} \]
Where \(\mathrm{scale(\gamma)}\) and \(\mathrm{offset}(\gamma)\) are
deterministic functions of \(\gamma\) chosen such that
\[
x \sim \mathcal{N}(0, 1) \Rightarrow
\mathrm{E}\left[f(x, \gamma)\right] = 0,
\mathrm{Var}\left[f(x, \gamma)\right] = 1
\]
- \(\gamma\) becomes a shape parameter that does not affect the
offset and scale of \(x\)
Choice of residual prior
\[
\epsilon_{ij} \sim t_\nu\left(0, \sigma^2_j\right)
\]
Where
\[ \begin{align}
\log \sigma_j &\sim \mathcal{N}\left(\mu_\sigma,
\sigma^2_\sigma\right) \\
\mu_\sigma &\sim \mathcal{N}\left(\log \mu_{\mu_\sigma},
\left(\frac{\log \sigma_{\mu_\sigma}}{1.96}\right)^2\right) \\
\log \sigma_\sigma &\sim \mathcal{N}\left(\log \mu_{\sigma_\sigma},
\left(\frac{\log \sigma_{\sigma_\sigma}}{1.96}\right)^2\right)
\end{align} \]
And e.g.
\[
\mu_{\mu_\sigma} = 0.8 \qquad
\sigma_{\mu_\sigma} = 1.5 \qquad
\mu_{\sigma_\sigma} = 0.3 \qquad
\sigma_{\sigma_\sigma} = 1.6
\]
- Hierarchical prior with feature-specific scale
- \(t\)-distributed residuals for robustness against outliers
Choice of parameter priors
\[ \begin{align}
\alpha_j &\sim \mathcal{N}(0, \sigma^2_\alpha) \\
\beta_j &= \mathrm{softplus}(\eta_j, \delta) \qquad
\eta_j \sim \mathcal{N}(\mu_\eta, \sigma^2_\eta) \\
\gamma_j &\sim \mathcal{N}(0, \sigma^2_\gamma)
\end{align} \]
Where e.g.
\[
\sigma_\alpha = 0.5 \qquad
\mu_\eta = -1 \qquad
\sigma_\eta = 0.7 \qquad
\sigma_\gamma = 0.5 \qquad
\delta = 1
\]
And
\[
\mathrm{softplus}(x, \delta) = \max(x, 0) + \log\left(1 +
e^{-\frac{|x|}{\delta}}\right) \, \delta
\]
Disease progression modeling
Latent disease progression model
\[
\theta_{i j} = \begin{cases}
h \left(
\left( \beta + b_i \right) \left( t_{i j} - \tau_i \right)
\right) +
u_{i j} &
i \in \mathrm{patients} \\
0 &
i \in \mathrm{controls}
\end{cases}
\]
\[
y_{k i j s} = \nu_k +
\lambda_k \theta_{i j} +
\epsilon_{k i j s}
\]
| \(t_{i j}\) |
Time since baseline for subject \(i\) at visit \(j\) |
Known |
| \(\theta_{i j}\) |
Disease severity |
Latent |
| \(\tau_i\) |
Disease onset relative to baseline |
Random effect |
| \(\beta + b_i\) |
Progression rate |
Fixed effect (population) + random effect |
| \(h\) |
Hinge or sigmoidal function |
|
| \(u_{i j}\) |
Per-visit severity baseline |
Random effect |
| \(y_{k i j s}\) |
Outcome \(k\) in walking segment \(s\) |
Known |
| \(\mu_k, \lambda_k\) |
Per-outcome intercept and slope (factor loading) |
Fixed effects |
| \(\epsilon_{k i j s}\) |
Residual error |
|
- Genetics-based disease onset estimates as priors?
- Pre-symptomatic patients? (censoring?)
- Outcomes not linear in \(\theta\)?
- Context covariates? (let them affect variance of \(\epsilon\)?)
TODO: Update this draft






















